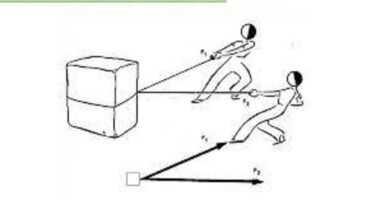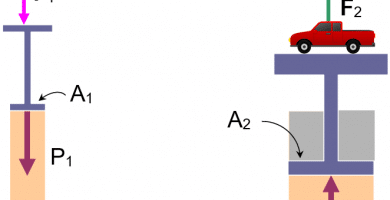
¿Qué dice la ley de pascal?

¿Cual es la formula de aceleracion?
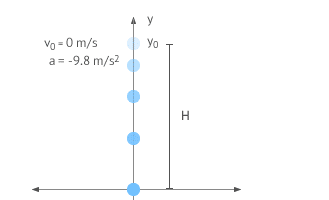
¿Qué es la Caída Libre?
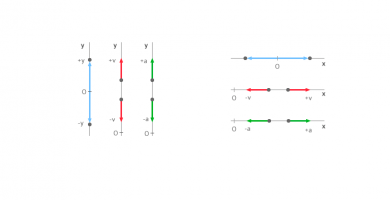
Encuentro en movimiento rectilíneo uniforme
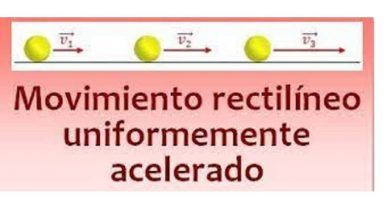
Aceleración en movimiento rectilíneo uniforme

¿Que son las revoluciones por minuto en física?
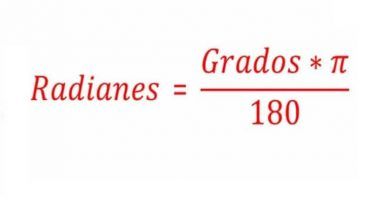
Conversión entre grados y radianes
¿Cuáles son las unidades de velocidad?

¿Que es velocidad media?
¿Cuál es la dirección y sentido de la velocidad?

¿Cuáles son las graficas de movimiento rectilineo uniforme acelerado?
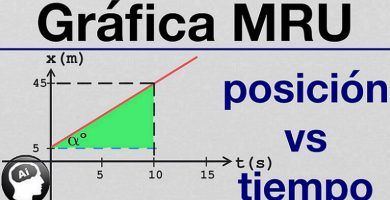
¿Cómo se elabora una grafica posicion vs tiempo?
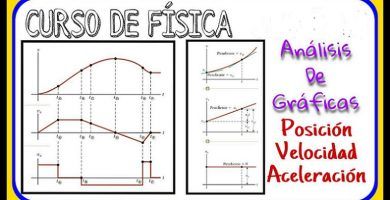
¿Cómo se elabora una grafica de posicion velocidad y aceleracion?
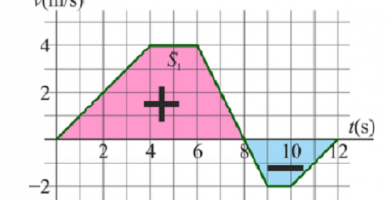
¿Como calcular la velocidad media de un tramo?
Tipos de desplazamiento
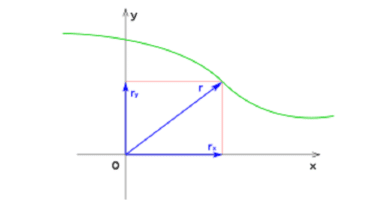
¿Que es la cinematica?
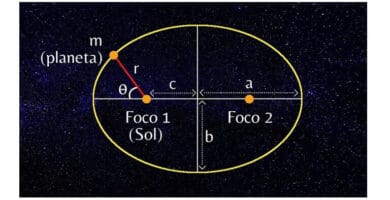
Leyes de Kepler

Segunda Condición de Equilibrio
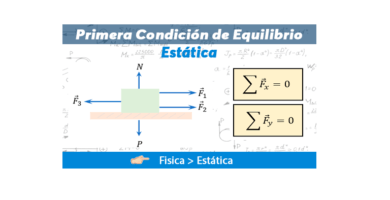
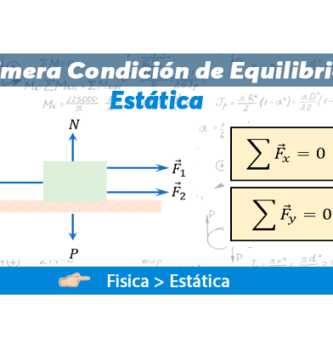
Primera Condicion de Equilibrio