En estática es fundamental conocer la primera condicion de equilibrio y la segunda condicion de equilibrio para entender la mecánica en Física.
VER VIDEO PRIMERA CONDICION EQUILIBRIO
Se frecuenta aprender las condiciones de equilibrio en fisica en niveles universitarios de ingeniería o la licenciatura de Física y Matemáticas. Pero en secundaria ya empezamos a lidiar con dichos tipos de inconvenientes.
Es por esa razón que este post vamos a describir los pasos para diagramar la primera condicion de equilibrio.
¿Qué es la primera condicion de equilibrio?
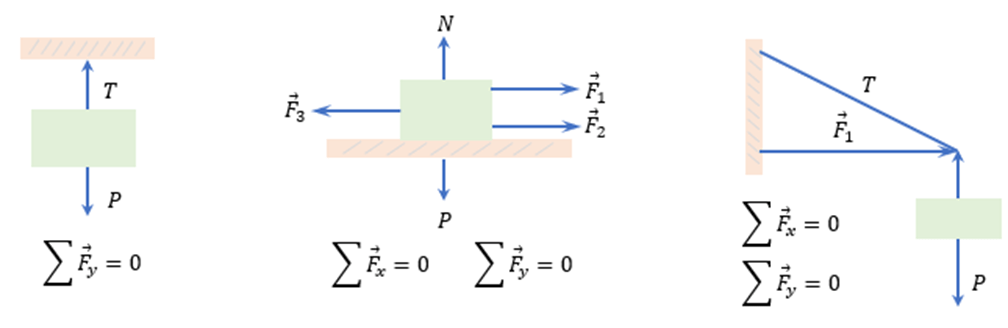
A continuación se muestra una gráfica que expresa la primera condición de equilibrio:
Viéndolo de otra forma, es como mencionar que la suma vectorial tanto en el eje “x”, como en el eje “y” tienen que sumar 0.
Es fundamental que en este punto domines realmente bien la descomposición vectorial en su forma rectangular.
Descomponer y sumar vectores por el método analítico
Para que un cuerpo este plenamente en equilibrio de traslación, la fuerza resultante que actúa sobre él debería ser igual a cero (0), es lo que dice la primera condición de equilibrio. Se deben considerar los pasos para dibujar un Diagrama de Cuerpo libre.
En términos matemáticos es decir:
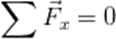
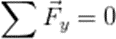
Para trabajar con este método precisamos lo siguiente:
1.- cada vector se deberá descomponer en componentes rectangulares
2.- Una vez realizado el paso 1, es significativo hacer la suma de componentes en “x” y “y” para cada uno de los vectores, para lograr tener un vector resultante de X y uno de Y con esto conseguiremos lograr el valor de la resultante final.
3.- Usar el teorema de pitágoras para hallar la magnitud resultante de los dos vectores perpendiculares.
4.- Usar la función tangente para determinar el ángulo respecto a la horizontal de la resultante.
Ejemplo 1: Encuentre la suma total de los vectores
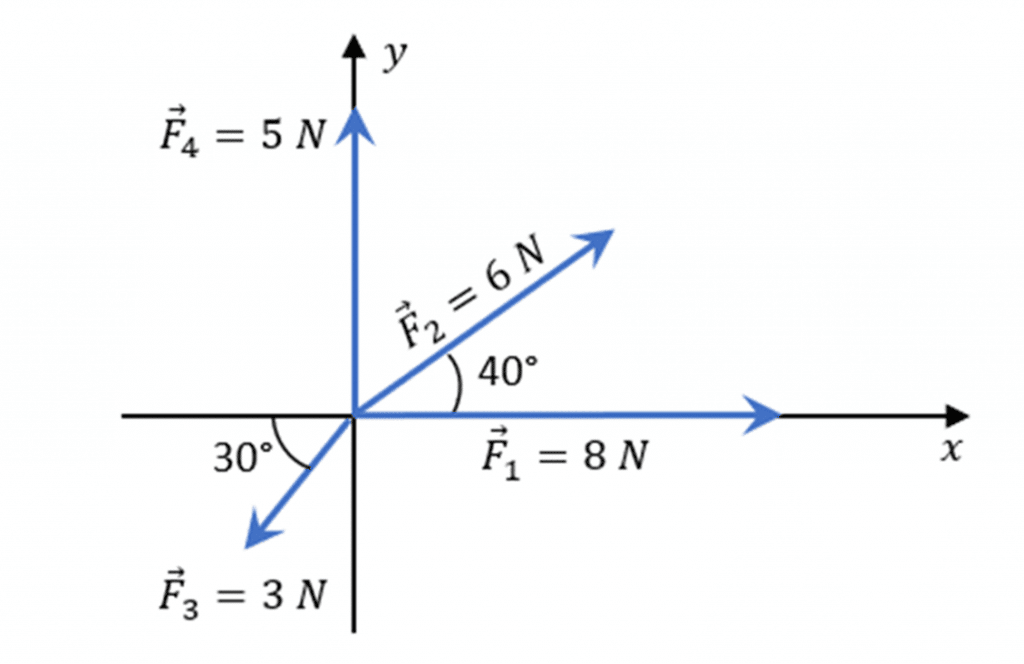
Vector F1
No tiene ningun componente en el eje “y”, solamente del eje “x” con esto logramos tener el primer valor para “x” una magnitud de 8N.
F1x=8N
Vector F2
El vector F2 tiene una magnitud de 6 N, y 40°, es decir; que tiene componentes “x” y “y”, por lo que lo descomponemos con funciones trigonométricas:
F2x=F2cos(40∘)=6cos(40∘)=4.596N
F2y=F2sen(40∘)=6sen(40∘)=3.856N
Vector F3
Este vector se puede observar que está en el cuarto cuadrante y con 30° respecto a la horizontal, por lo que sus componentes serán negativos tanto para “x” como para “y”
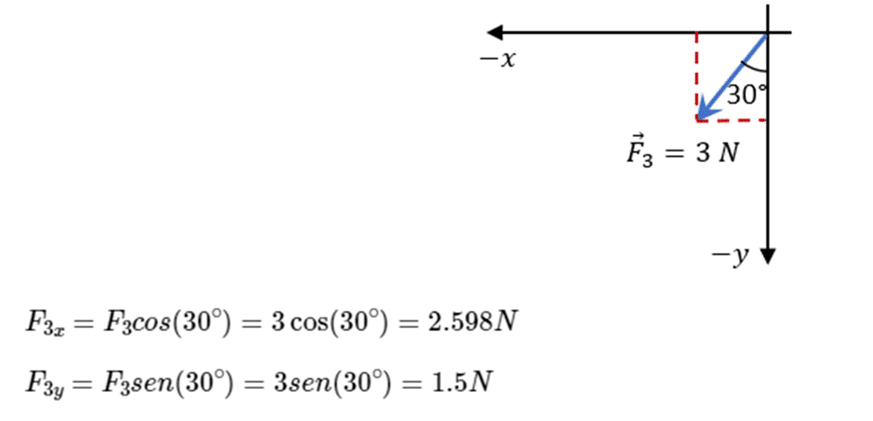
Se debe modificar el signo a los valores de las componentes
F3x=−2.598N
F3y=−1.5N
Vector F4
Este vector unicamente tiene componente en “y”, es decir una magnitud de 5N
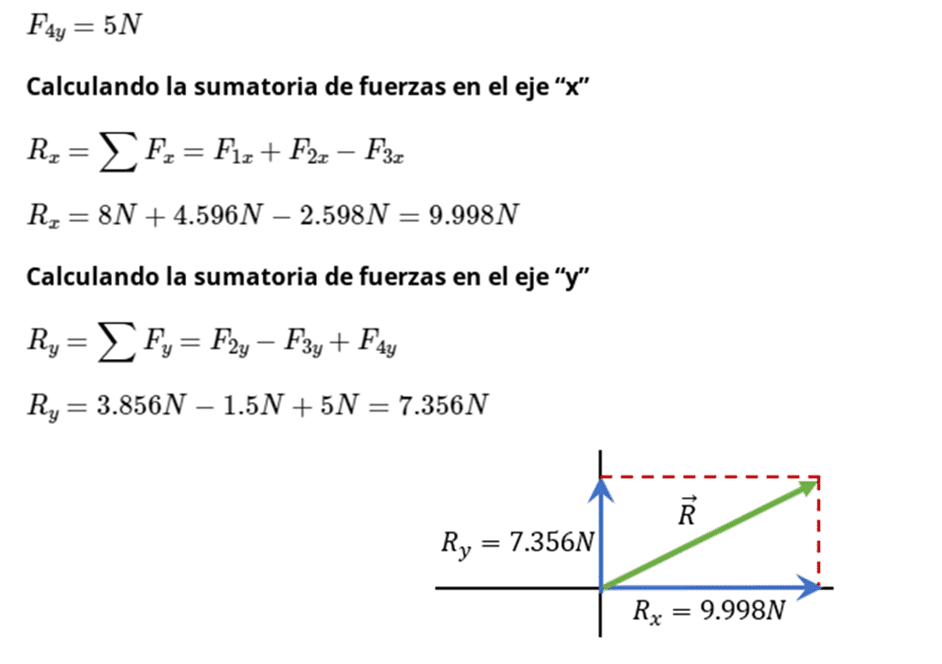
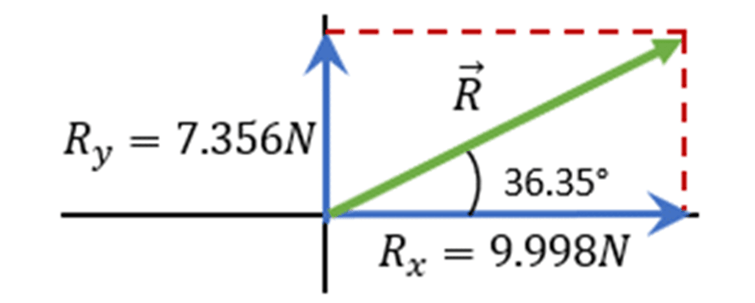
Obteniendo la resultante
Aplicando el teorema de pitágoras
R=Rx2+Ry2
R=(9.998N)2+(7.356N)2
R=154.07N2
Por lo que
R=12.41N
Qué sería nuestra magnitud.
Angulo de la resultante:
Aplicamos la tangente (cateto opuesto/cateto adyacente) para obtener el ángulo.
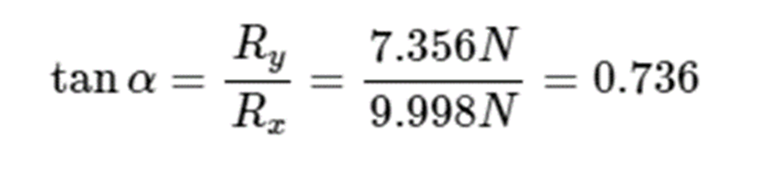
aplicamos el arcotangente
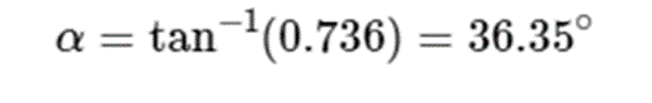
Por lo que tendríamos un ángulo de 36.35° de la resultante respecto a la horizontal.
Pasos para dibujar un Diagrama de Cuerpo libre en la primera condicion del equilibrio
Es bastante difícil solucionar un problema de estática si no se traza un diagrama de cuerpo libre del problema, con el DCL (Diagrama de Cuerpo Libre) tenemos la posibilidad de aislar un cuerpo y exportarlo a un plano cartesiano para examinar las fuerzas que trabajan sobre el cuerpo.
Los pasos para dibujar este tipo de diagramas dentro de la primera condición de equilibrio, son los próximos:
Primer Paso: Excluya el cuerpo del problema y trace cada una de las fuerzas que trabajan sobre él, con ello damos el inicio fundamental para la solución de nuestro problema.
Paso 2: Se trazará sobre un plano cartesiano y se procederá con una descomposición de los vectores en su forma rectangular.
Tercer 3: Coloque correctamente las fuerzas ya descompuestas, así como además los ángulos.
Cuarto 4: Aplique las ecuaciones de condición de equilibrio, para obtener las incógnitas deseadas.
Ejemplo Primera Condición de Equilibrio