Ley de kepler. Publicamos sobre el asunto de la gravitación mundial y resolvimos ejercicios que hicieron que comprendiéramos mucho mejor el asunto de la atracción gravitatoria entre los planetas, puesto que bien hasta allí todo bien. Empero para profundizar mejor el asunto, poseemos que retroceder un poco al tiempo, o sea, muchísimo más anterior a la aparición de las leyes de Newton, y nos remontemos al análisis de los planetas y sus movimientos, para conocer a fondo las Leyes de Kepler. De esta forma que toma asiento, y prepárate para comprender la breve historia y a solucionar ejercicios.
Empecemos hablando del astrónomo Johannes Kepler (1571-1630) , Kepler ha sido un espectacular y brillante astrónomo alemán, que aprendió de las enseñanzas tanto de Nicolás Copérnico como de Tycho Brahe, tanto que le produjo bastante interés en conocer como se movían los planetas en torno al Sol, y que luego de una tediosa averiguación ha podido confirmar que los plantes no se movían en forma circular, sino que se movían describiendo órbitas elípticas. Las cuales le permitió entablar diversos enunciados matemáticos, involucrados con el sistema solar, y de esta forma poder formular 3 leyes sobre el desplazamiento de los planetas, conocidos como las leyes de Kepler.
Sin embargo, milenios atrás ya había mucho análisis relacionado al desplazamiento de los planetas y las estrellas. Ejemplificando durante el siglo II d.C, el griego Claudio Ptolomeo había postulado la teoría de que la tierra era el centro del mundo, esto paso a ser el célebre modelo geocéntrico, tiempo después al rededor del siglo XIV y comienzos del siglo XV el astrónomo Nicolás Copérnico ha sido capaz de mostrar que los planetas incluida la tierra en verdad se movían en órbitas circulares al rededor del Sol. Aun cuando ésto carecía de exactitud tuvo que llegar el astrónomo danés Tycho Brahe donde perfeccionó las mediciones sobre el desplazamiento de los planetas. Puesto que para aquel entonces el telescopio no se había descubierto.
La Ley de Kepler se publico en el año 1609, curiosamente aquel mismo año el físico Galileo Galilei construyó su primer telescopio.
Primera Ley de Kepler
La primera ley de Kepler o además llamada como la ley de órbitas, muestra lo próximo: Los planetas se mueven en órbitas elípticas, con el Sol en uno de los aspectos focales. Veamos la siguiente imagen que explica el primer enunciado.
El punto de la órbita más cercano al Sol se le conoce como perihelio y el punto más lejano se le llama afelio, las elipses tienen una forma ovalada o de círculo aplanado, el ancho de aquel círculo achatado se le conoce como “excentricidad”, la parte que está sobre el eje “x” se le llama eje más grande, y del eje “y” se le conoce como eje menor.
Segunda Ley de Kepler
La segunda ley de Kepler o además llamada como la ley de zonas , es aquella ley que enuncia lo próximo; Una linea del Sol a un mundo barre zonas equivalentes en periodos de tiempo de tiempo equivalentes. Veamos la imagen que lo explica mejor.
Esta ley nos sugiere que la velocidad orbital de un mundo cambia en diferentes punto de su órbita. Ya que la órbita del mundo es elíptica, su velocidad orbital es más grande una vez que está más cerca del Sol que una vez que está más lejos. Curiosamente Newton después mostró que esto era efecto de su ley de la gravitación mundial.
Tercera Ley de Kepler
La tercera ley de Kepler o además famosa como la ley de periodos , es una ley que instituye que el cuadrado del lapso orbital de un mundo es de forma directa proporcional al cubo de la distancia promedio entre el mundo y el Sol; o sea que:
Es simple deducir la fórmula de la tercera ley de Kepler, desde la ley gravitacional de Newton, e igualando con la fuerza centrípeta que procede de la fuerza de gravedad. Teniendo presente esto, entonces mencionamos que:
Fuerza Centrípeta = Fuerza Gravitacional
Entonces:
![]()
Dónde:
mp = Masa del mundo
Ms = Masa del Sol
r = distancia
G = constante gravitacional
Despejando a la rapidez “v”, poseemos que:
![]()
Sin embargo como la rapidez es distancia sobre tiempo, y tenemos la posibilidad de interpretarla como la distancia del círculo (2πr) sobre el Lapso (tiempo que tarda en ofrecer la vuelta).
![]()
Vamos a despejar al lapso “T”
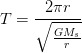
Elevando al cuadrado los dos miembros, poseemos que:
Dejando fuera a r^3, poseemos que:
![]()
De aquí tenemos la posibilidad de tomar a lo próximo como una constante, la constante de Kepler:
![]()
Podemos inclusive, reescribir nuestra fórmula de la siguiente forma:
![]()
Ejercicios leyes de kepler
Para centrarnos en los ejercicios, tomaremos la fórmula de la tercera ley de Kepler que nos va a servir para calcular ciertos datos, veamos entonces una ejemplificación.
Ejemplo 1.- El mundo tierra tiene un satélite natural denominado “Luna”, Pues la luna está a una distancia promedio de 384,400 km de la tierra, y tiene una época orbital de 27 días, calcule la masa de la tierra.
Solución.
El problema nos da ciertos datos relevantes como la distancia “r” y el costo del lapso “T”, por lo cual tenemos la posibilidad de calcular el costo de Kt, esto podría ser en unidades del Sistema Universal, de esta forma que veamos:
Procedemos entonces al cálculo de K
De allí poseemos que:
![]()
![]()
![]()
Entonces, tenemos la posibilidad de despejar de la fórmula de Kepler para la masa de la tierra:
![]()
De aquí despejamos a Mt
Entonces, la masa de la tierra es:
![]()
Vendría a ser un aproximado, sin embargo podría ser la forma adecuada de hacer el cálculo de la masa de la tierra.
