Como todos sabemos existen condiciones de equilibrio en fisica, hasta este punto es bastante seguro que ya estudiaste la primera condición de equilibrio, por lo que ahora veremos la segunda condicion de equilibrio.
Luego de entender esa condición es elemental conocer la 2da condicion de equilibrio, esa condición se produce una vez que comentado desplazamiento está girando sobre su mismo eje.
¿Cual es la segunda condicion de equilibrio?
La segunda condicion de equilibrio que dice: la suma de los instantes o torques de las fuerzas que trabajan sobre el cuerpo en relación a cualquier punto tienen que ser igual a cero.
Para comprender la segunda condición de equilibrio, debemos rememorar el inicio de la primera condición.
Así como un cuerpo puede quedar en equilibrio de traslación si la resultante de fuerzas que trabajan sobre el cuerpo es cero, lo mismo pasa una vez que un cuerpo está girando sobre su mismo eje.
Segunda condicion de equilibrio ¿Qué es dos Fuerzas?
Para la segunda condición de equilibrio, es fundamental conocer la definición de par de fuerzas.
Un par de fuerzas sucede cuando existen 2 fuerzas que trabajan sobre un cuerpo, son fuerzas paralelas, de misma intensidad y sentido opuesto, la resultante es igual a cero y su punto de aplicación está en el medio de la línea que junta los puntos de aplicación de las fuerzas que lo conforman.
Se puede mirar el ejemplo, en un disco sometido a dos fuerzas para la segunda condicion de equilibrio.
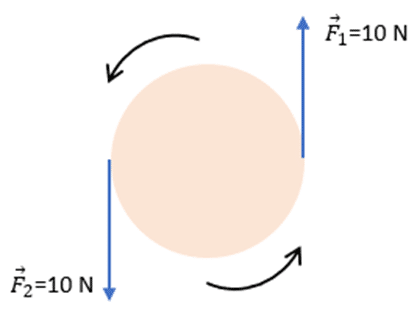
Si queremos descubrir la fuerza resultante en el disco, bastaría con mirar el sentido del par de fuerzas.
La fuerza F1 va hacía arriba lo que suponemos como positivo (+), en lo que la fuerza 2 F2 va en dirección contraria, lo cual consideraríamos como (-). lo cual nos proveería el costo de cero. O sea, el disco no se mueve.
¿Qué es un Momento? o ¿Qué es un Torque?
Frecuentemente escucharemos el concepto de Torque o momento. Los dos términos son lo mismo y esa definición radica en aquella fuerza capaz de hacer girar un cuerpo.
No obstante esa definición además incluye una ecuación matemática:
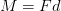
Dónde:
M = De una fuerza el momento
F = Fuerza aplicada
d = Distancia (brazo de palanca)
El momento se mide en unidades de (Nm)
Aun cuando es un asunto importante para entender la estática, es fundamental que se estudie los casos que tenemos la posibilidad de encontrarnos al calcular los instantes. Veamos 4 casos habituales.
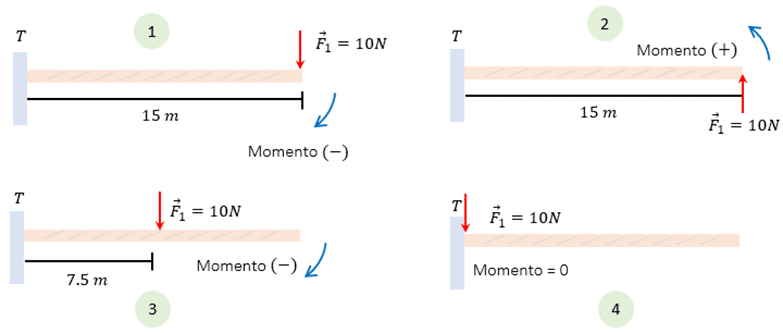
De los 4 casos aquí expuestos, tenemos la posibilidad de aprender mucho con examinar todos ellos y tomar en consideración lo próximo:
- El momento aplicado tiene que partir de un punto en común, en dichos ejemplos todos toman un punto de apoyo que vamos a llamar T
- En la situación 1 y 2 la viga es sometida a fuerzas equivalentes sin embargo con distinto sentido y la distancia es la misma.
- En la situación 3, pese a que la fuerza es la misma, el brazo de palanca o “distancia” se toma ejecuta a la mitad.
Teniendo presente dichos puntos de vista, vamos a puntualizar otro punto fundamental.
El momento de una fuerza es positiva si su tendencia de giro en relación a un cuerpo es en sentido opuesto al giro de las manecillas del reloj.
Si queremos hallar el Instante de cada fuerza lo haríamos de la siguiente forma:
Caso 1 rotacional:
Para esta situación, basta con mirar el brazo de palanca existente a partir de donde está la fuerza hasta el punto de apoyo T , hay 15 metros y además una fuerza de 10N.
Tomando en cuenta que un rato es positivo si la fuerza señala en dirección contraria a las manecillas del reloj, y negativo si gira en dirección horaria, entonces sabremos que es un rato negativo.
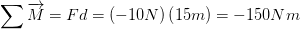
Caso 2: 2da condicion de equilibrio fisica
La exclusiva diferencia del caso 1, es que la fuerza está en dirección contraria a las manecillas del reloj, por lo cual tendremos un rato positivo. En otras palabras matemáticamente:
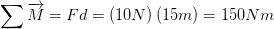
Caso 3 :
En la situación 3, vemos precisamente que la fuerza está en dirección de las manecillas del reloj, por lo que es negativa, y la distancia donde se aplica la fuerza es a mitad del punto de apoyo T, entonces mencionamos que:
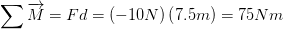
Caso 4: 2 condicion de equilibrio
Esta situación es fundamental, al no haber ningún brazo de palanca “distancia” es lógico que la viga no va a tener ni una actitud de fuerza, debido a que está justamente en el punto de apoyo, ahora matemáticamente podríamos explicarlo de esta forma:
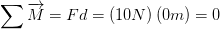
Ejercicios de la segunda condicion
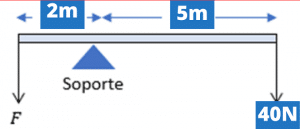
En este caso, el eje de rotación se encuentra en el soporte, se debe considerar el sentido de la fuerza, para el torque número uno vemos que nos encontramos a F pero tiene que girar en sentido contrario a las manecillas del reloj, hacía el soporte entonces será positivo (+).
r1=(F)(2m)=2F
En el caso del torque número dos, la fuerza de 40 N se ubica del lado derecho del soporte por ende el giro será en el mismo sentido que las manecillas del reloj y esto hará que se convierta en negativo.
Utilizando las fórmulas de la segunda condición de equilibrio tenemos:
∑r=0 r1+r2=0
r2=-(40N)(5m)=-200Nm
Al reemplazar los diferentes datos en la fórmula se encontrará:
2F + (-200Nm)=0
2F -200Nm=0
Despejando a 2F
2F =200Nm
F =200Nm/2= 100Nm
Por lo que la magnitud de la fuerza para que el sistema se encuentre en condiciones de equilibrio total es de F = 100 Nm como se puede ver en los ejemplos de la segunda condicion de equilibrio.
