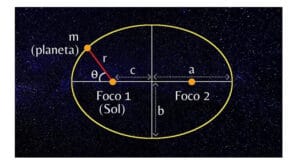
La mecanica de cuerpos rigidos es la rama de la física que estudia la naturaleza del desplazamiento de los cuerpos, y su evolución en la época, bajo la acción de cargas. Para entender la mecanica de cuerpos rigidos es recomendable leer los diferentes artículos de este blog como la realización de Cursos de Nivelación previos. Paralelamente, en la mecánica tenemos la posibilidad de hacer una primera exclusión entre:
Cinemática: especificación matemática y geométrica del problema. Es la rama de la mecánica que estudia el desplazamiento de los cuerpos sin que importe las razones que lo producen.
Dinámica: leyes físicas que gobiernan los movimientos. Es la rama de la mecánica que estudia el desplazamiento de los cuerpos prestando atención a las razones que lo producen (cargas actuantes).
Según el título de este capítulo, nos centraremos en incorporar entonces los conceptos básicos concernientes al análisis de la mecánica de sistemas de cuerpos rígidos, los cuales van a ser usados para abordar la exploración presentado en este trabajo. Antecedente de empezar a dialogar de lo cual es un «sistema de cuerpos sólidos» resulta adecuado conceptualizar primero que significa «cuerpo rígido».
CUERPO RIGIDO
Un cuerpo humano tieso es un ente ideal, y se define como un sistema formado por infinitas partículas tales que las distancias relativas en medio de las mismas se preserva inalterable en la era, o sea que no sufre deformaciones independientemente de las cargas que actúen sobre el mismo. Hablamos de un ente ideal, debido a que las construcciones y máquinas reales jamás son definitivamente rígidas y se deforman bajo la acción de cargas que trabajan sobre ellas. No obstante, si las deformaciones que sufre un cuerpo humano son pequeñas comparadas con las magnitudes del mismo, y si la disipación de energía vinculada a efectos flexibles es despreciable, entonces la suposición de cuerpo humano tieso podría ser empleada sin inconvenientes.
SISTEMAS DE CUERPOS RIGIDOS
Un «sistema de cuerpos rigidos» es un sistema compuesto por un grupo de diversos cuerpos diferentes vinculados entre sí mediante diversos tipos de uniones. A diferencia de los cuerpos firmes relacionados, las uniones que los conectan tienen la posibilidad de integrar diversos tipos de elementos no firmes, como por ejemplo resortes o amortiguadores. Para una especificación completa de un sistema de cuerpos sólidos se necesita especificar una enorme proporción de límites entre los cuales tienen la posibilidad de nombrar:
- Número de cuerpos
- Composición de interconexiones entre los diversos miembros del sistema.
- Limitaciones cinemáticas
- Localización y propiedades de las uniones en cada cuerpo humano.
- Masa e inercia de cada cuerpo humano.
ECUACIONES DE DESPLAZAMIENTO
La finalidad de este trabajo es formular las ecuaciones de desplazamiento de un sistema de cuerpos rígidos y obtener su solución por medio de técnicas numéricas. Las ecuaciones de desplazamiento, o sea, las ecuaciones diferenciales que definen el estado del sistema, tienen la posibilidad de obtener mediante diferentes enfoques, como por ejemplo:
- Leyes de Newton
- Inicio de D’Alembert generalizado
- Comienzo de Hamilton
- Ecuaciones de Lagrange
- Ecuaciones de Hamilton
Las leyes de Newton son la base de la llamada Mecánica Vectorial. En ésta el desplazamiento se examina mediante entidades como por ejemplo fuerzas y instantes, las dos porciones vectoriales. Una formulación plenamente distinto exitosa como Mecánica Lagrangiana o Analítica, expone los inconvenientes de la dinámica en términos de porciones escalares, como la energía potencial y cinética. A ésta pertenecen el inicio de Hamilton y las ecuaciones de Lagrange y Hamilton. La mecánica analítica condujo al desarrollo de herramientas matemáticas poderosas como el «Cálculo de Variaciones». Esta forma opción de obtener las ecuaciones de desplazamiento se sabe como formulación variacional de las ecuaciones de desplazamiento.
Breve reseña de las leyes de Newton:
1ª Ley de Newton: Todo cuerpo humano persevera su estado de reposo o desplazamiento uniforme y rectilíneo a no ser que sea obligado a modificar su estado por fuerzas impresas sobre él. Con esta primera ley, Newton metió el término de sistema inercial o newtoniano con respecto al cual tenemos la posibilidad de calcular.
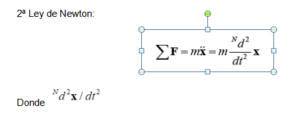
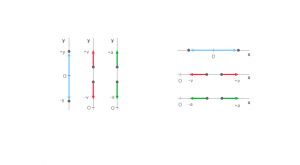
es la derivada segunda del vector x respecto al tiempo, desarrollada por un observador situado fijo al marco de alusión inercial N. Un marco inercial es entonces un sistema de alusión con respecto al cual cuerpos aislados se mueven online recta y a rapidez constante. A este marco inercial N se le adhiere una terna de vectores unitarios: (nˆ1, nˆ2,nˆ3) , los cuales definen una «base» ortonormal y dextrógira. Por consiguiente, dichos vectores satisfacen continuamente las próximas características:
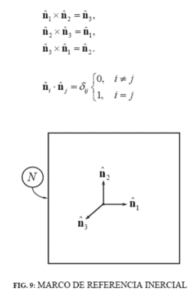
Es fundamental ilustrar que dichos vectores unitarios solo definen direcciones. No obstante, si se desea hacer mediciones va a ser primordial «pegarle» a esa base un sistema de coordenadas, de la misma forma que un sistema rectangular cartesiano ortogonal (X,Y,Z):
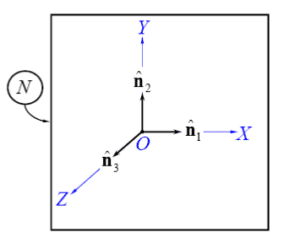
FIG. 10: MARCO INERCIAL MÁS SISTEMA COORDENADO CARTESIANO
3ª Ley de Newton: Para toda acción existe constantemente una actitud igual y contraria: o sea, que las actividades mutuas de 2 cuerpos constantemente son equivalentes y dirigidas en sentido contrario.