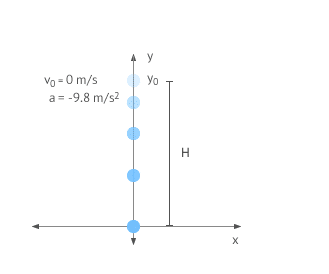De entre todos los movimientos rectilíneos uniformemente acelerados (mrua) o movimientos rectilíneos uniformemente variados (mruv), existen dos de particular interés: la caída libre y el lanzamiento vertical. En este apartado estudiaremos la caída libre. Ambos se rigen por ecuaciones propias de los movimientos rectilíneos uniformemente acelerados:
y=y0+v0*t+0,5*a*t^2
v=v0+a*t
a=constante
Caída Libre
Desde cierta altura H en la caída libre un objeto cae verticalmente despreciando cualquier tipo de rozamiento con el aire o cualquier obstáculo. Se trata de un movimiento rectilíneo uniformemente acelerado (mrua) en el que la aceleración coincide con el valor de la gravedad. Dentro de la Tierra, la aceleración de la gravedad se puede considerar constante, se designa por la letra g y su valor es de 9,8m/s^2.
Usemos un sistema de referencia para el movimiento de caída libre cuyo origen de coordenadas se encuentra en la vertical del punto desde el que soltamos el cuerpo y consideraremos el sentido + del eje y apuntando hacia arriba.
Sistema de Referencia en Caída Libre
Es normal usar un sistema de referencia a la hora de resolver este tipo de problemas. El cuerpo siempre se encuentra sobre el eje Y posítivo, e inicialmente su posición yo=H, su velocidad es 0 metros por segundo (parte del reposo) y su aceleración es constante e = a la gravedad pero con signo – ya que la tendencia del movimiento es contrario al sentido del eje y. Ten en cuenta que los valores de velocidad que obtengas serán negativos.
Con todo esto nos quedaría:
v0=0; y0=H; a=-g
La caída libre en el que se deja caer un movimiento rectilíneo uniformemente acelerado (mrua) un cuerpo verticalmente desde cierta altura y no encuentra resistencia alguna en su camino. Las ecuaciones son:
y=H-0,5*g*t^2
v=-g*t
a=-g
Donde:
- y: La posición final del cuerpo. Su unidad es el metro (m)
- v: La velocidad final del cuerpo. Su unidad es el metro (m/s)
- a: La aceleración del cuerpo en el movimiento. Su unidad es m/s^2 el metro por segundo al cuadrado.
- t: Intervalo en el que se produce el movimiento. Su unidad es el segundo (s)
- H: La altura desde la que cae el cuerpo. Se mide en metros al tratarse de una medida de longitud.
- g: El valor de la aceleración de la gravedad, en la superficie terrestre es 9.8 m/s^2
Experimenta y Aprende
H
t(s) = 0,0
La bola azul
La bola azul representa un cuerpo suspendido sobre el suelo. Puedes arrastrarlo hasta la altura inicial H que desees y a continuación pulsar el botón para dejarlo caer.
Observa que, una vez iniciada la simulación, puedes deslizar el tiempo y ver como, bajo la etiqueta Datos, se calculan los valores de posición y velocidad correspondientes, en el camino del cuerpo hacia el suelo.
Datos
H = 40 m
y = H-(1/2)*g*t^2 = 40 – 0,5*9.8*0.002 = 40 m
v = -g*t = -9.8*0.00 = 0.00 m/s
g = 9.8 m/s^2
Puede que te estés preguntando si entiendes las fórmulas que hemos visto hasta ahora, ¿Dónde está la masa? El sentido común nos dice que un cuerpo pesado, por ejemplo, un martillo, debería caer a mayor velocidad que un cuerpo ligero, como una pluma. No acierta en esa ocasión el sentido común. Es que si la pluma y martillo estuvieran en el vacío, ambos caerían a la misma velocidad. Su efecto es más evidente sobre la pluma, que llegará al suelo más tarde cuando no están en el vacío y el aire se encuentra ofreciendo resistencia a estos cuerpos.